Supp. Info. for the Singh et al., ICML 2005 submission is here.

An important open problem in designing time-series microarray experiments is choosing the number of time-points to observe and when to make the observations. A good experimental design strategy will optimize the quality of data obtained from such studies while minimizing the number of observations. We developed an online algorithm for time-series experiments that allows an experimenter to determine which biological samples should be hybridized to arrays to recover expression profiles within a given error bound. The algorithm uses generalized cross validation to determine when sufficient observations have been made to meet the given error bound and if the bound is not met, determines where in the time domain the next sample should be observed. Our active learning approach takes into account both the global and local structure of the time-dependent expression profile when suggesting a new sample to hybridize, and requires almost no previous knowledge of the underlying biological system to determine effective sampling strategies.

This webpage contains material relevant to this project. In particular, it contains supplementary material for the following paper

Singh R, Palmer N, Gifford D, Berger B and Bar-Joseph Z. Active Sampling for Sampling in Time-Series Experiments: With Application to Gene Expression Experiments Proceedings of the 22nd Int'l Conference on Machine Learning, 2005. To Appear.

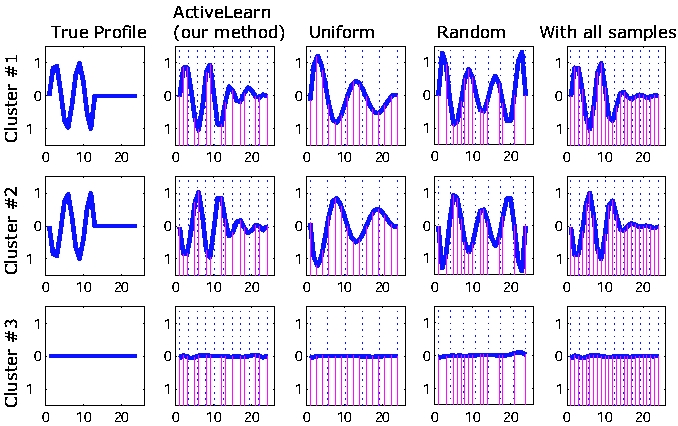
Example Scenario: we re-generate expression profiles for 150 genes (grouped into 3 clusters) by using various sampling strategies. The true profile, per cluster, is shown in the first column. A total of 24 sampling locations are potentially available. Columns 2-4 depict the performance of different sampling strategies when only 15 of these locations are actually chosen. The location of sampled time-points is indicated by the solid supporting bars (from X-axis to the curve). The fifth column shows results achieved by using all 24 samples. As can be seen, our sampling strategy (second column) performs much better than random sampling or uniform sampling, even with the same number of samples.

Code Availability: Prelimary version of the MATLAB code can be downloanded here in a .tar.gz format. Brief instructions for running the code are available in the README file included in the distribution. For more detailed instructions on how to run the code please email us.