Supplementary Information for Singh et al. ISMB'05 submission

Supplementary Information for:

Singh R, Palmer N, Gifford D, Berger B and Bar-Joseph Z. Active Sampling for Sampling in Time-Series Experiments: With Application to Gene Expression Experiments Proceedings of the 22nd Int'l Conference on Machine Learning, 2005. To Appear.

Details on Continuous Representations of Time Series Microarray Data: In previous work, we describe a method for representing expression profiles using aligned continuous curves [Bar-Joseph et al, 2002]. In this paper, we use our continuous representation and alignment algorithms as a pre-processing step in order to make time series experiments comparable when these experiments have different sample rates and variations in the timing of the underlying biological process. We briefly outline this pre-processing step here.

To obtain a continuous time formulation, we use cubic B-splines, which are sets of piecewise defined cubic polynomials, to represent temporal gene expression profiles. Splines in general, and cubic B-splines in particular, are mathematically convenient for data approximation are often used to produce smooth low-degree polynomial curves, while avoiding the problems of overfitting, numerical instability and oscillations that arise if single high-degree polynomials are used.

B-splines are described as a linear combination of a set of basis polynomials. By knowing the value of these splines at a set of control points, one can generate the entire set of polynomials from these basis functions. We assume that the expression of gene at time can be represented by a spline curve and additional noise using the following equation:

$\begin{displaymath} Y_{i} = S F_i + \epsilon_i \end{displaymath}$

(1)

Here is the expression profile for gene , is a vector of spline control points for gene and is a matrix of spline basis functions evaluated at the sampling points of the experiment. $\epsilon_i$ is a vector of the noise terms, which is assumed to be normally distributed with mean . Because the data is expected to be noisy, and may contain missing values, determining the parameters of the above equation ( and $\epsilon_i$ ) for each gene separately may lead to overfitting. Instead, when estimating these splines from expression data, we constrain the control point values of genes in the same cluster (co-expressed genes) to co-vary, thus using other co-expressed genes to overcome noise and missing values for a single gene. The parameters of this model are determined using an EM algorithm. In the E step we determine cluster membership for each gene, while the other parameters of the model are maximized with respect to cluster assignment in the M step. See [#!BGGJS03!#] for complete details.

Given the spline coefficient matrix, , in the above model, for a data set containing time-points when control points are used, the smoothing matrix is defined as:

$\begin{displaymath} A=S(S^TS)^{-1}S^T \end{displaymath}$

(2)

where is a $k\times p$ matrix. Thus rows of define the ``coordinates'' of the time-points in terms of the basis splines.

In previous work [Bar-Joseph et al. 2002], we showed that this method provides a superior fit for time series expression data when compared to all other previous methods.

Figure: (a): Confidence Intervals estimated using LCV or GCV: in both figures, sampled time-points are marked with dots; the true curve is shown in a dashed line; the estimated curve is shown in a solid line; and the GCV and LCV based confidence intervals are plotted for each sampled time-point. In this case, the only difference is that the smoothing parameter is the same for both the curves (

). As a result, the relative sizes of GCV-based confidence intervals is the same for both curves. However, the profile on the right has more local variation. This can be captured using LCV, which results in confidence intervals that are larger in this region of uncertainty. (b): Definition of confidence area for a curve. It is the area between the

and

, the two curves in dashed lines. We approximate as the sum of the area of trapezoids joining the CIs at each sampled point (thin solid line).

[] $\includegraphics[width=3.4in]{methods1_t8_fig1.eps}$

[] $\includegraphics[width=1.8in]{methods2_t8_fig2.eps}$

Generation of Simulated Data:

**Figure:** Three different datasets generated for simulations: Each dataset has 150 genes grouped into 3 clusters. The cluster-specific curves are shown in bold line. Behind these curves, in each box, 50 gene-specific curves are shown in thin lines. See the text for more details. The hardness of a dataset is controlled by increasing the frequency of the sinusoidal component or introducing flat segments. For example, dataE is harder than dataA because, even though the frequency is the same, it is possible to use fewer time-points for dataE than dataA, by focusing only on the non-flat region. The hardest dataset, dataI, has both higher frequency and a significant flat part.
$\includegraphics[width=4.5in]{sim_dAEI_ai.eps}$

We generated many datasets, with varying levels of ``hardness''. Here, we show three of these; others are listed below. Each of the dataset has 150 genes, distributed equally in three clusters. Sinusoidal curves and flat lines are used to construct the per-cluster profiles, to which some random noise is added to generate gene-specific profiles (see Appendix for more details). Expression profile for each gene is randomly chosen from a Normal distribution centered at the cluster-specific profile. This cluster-specific function represents the gene's true expression profile while the random variations represent experimental errors. One of the clusters always has a flat expression profile. The other two are a combination of sinusoidal curves with flat lines, with the sinusoidal curves being possibly damped. The amplitude of sinusoidal curves is always 1. The frequency of the sinusoidal curves and their positions across the two clusters are used to control how hard a dataset is: higher frequency implies that more time-points will be needed to characterize the curve fully. Given this cluster-specific function, the expression profile for each gene is the sum of this function with some Gaussian noise with a standard deviation of 0.2 (

). To produce discrete observations, these curves were then sampled at 24 equally spaced time-points, thus producing a 150 $\times$ 24 matrix of observations. Our goal is to use observations at only a few of these 24 time-points to re-generate the true expression profiles.

The hardness of a dataset is controlled by varying the frequency of sinusoids and their positions across the clusters: higher frequency implies that more time-points will be needed to characterize the curve in that region. Also, introducing flat regions makes the dataset harder in the opposite way: if we require that sampling strategy use fewer time-points in total, then it will then have to find out a way to identify flat regions and sample at a low rate there.

Plots for some other generated datasets are shown here:

Easy: dataA, dataD
Moderate: dataE, dataH
Hard: dataB, dataI

Generalized Cross Validation(GCV) as an approximation to Cross Validation(CV): For 5 datasets, 16 sets of timepoints were randomly generated with each set having 6-20 timepoints. Of the total 80 runs, there were run-time errors or non-convergence in 16, leaving 64 runs for which we compared the performance of GCV vs. CV. In both cases, we computed the optimal number of control-points required to create the continuous representation of the simulated observations. This number was compared across GCV and CV. Also, in the case of GCV, three different cost weights- 0.8, 0.9, 1.0- were used. As our adpative cost strategy allows us to choose the most appropriate cost term "c" for the data, we compared CV against the best choice of cost weight for GCV per run. This figure shows the absolute difference between the number of control points predicted by GCV and CV, plotted as a frequency distribution. As it shows, in most cases GCV and CV agree exactly on the number of control points. In more than 90% of the cases, the absolute difference is atmost 2. Thus, GCV is a good approxmation to CV. Moreover, as the paper mentioned, it takes almost an order of magnitude less time to run (3.19 hours vs. 31 min)
Adaptive Cost Strategy for GCV: While the GCV scoring function performs well on average, it may sometimes undersmooth/oversmooth the estimated curve. If prior information about the true shape of the underlying function is available, it can be incorporated using a cost term $\mathcal{C}$ . $\mathcal{C}<1$ encourages larger (better fit) while $\mathcal{C}>1$ encourages smaller (more smoothing). Our simulations indicated that only the former ( $\mathcal{C}<1$ ) was necessary, if at all. Furthermore, Wahba's formulation assumes that $\mathcal{C}$ can be chosen using prior information. For cases when no such information is available, we have extended the GCV formulation by introducing the adaptive cost strategy.
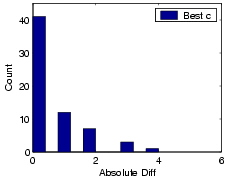
The adaptive cost strategy is quite intuitive: if the addition of new data doesn't change , decrease the cost a bit; otherwise, set it back to the default value (= 1). More precisely,

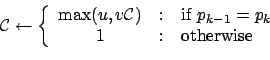
$\begin{displaymath}\mathcal{C} \leftarrow \left\{ \begin{array}{c@{\quad:\quad}l... ...{if } p_{k-1}=p_k \\ 1 & \mbox{otherwise} \end{array} \right. \end{displaymath}$

where and is the optimal for time-points. Our experiments indicated that values of and worked well for many datasets.
Fig 2(a) in the paper showed how our method outperforms random sampling. For each of the datasets generated by simulation, we visually depict the quality of sample-sets chosen by our method vs. those from random sampling (across 10 tries of random sampling). Each figure shows the results of our method (marked by "lcv+al") as compared to results from 3 of the random tries. The arrangement of columns inside the figure is the same as that of Fig 1 in the paper:
A fuller description of how the FCOMB set, described in Section 5.3 page 8 of the paper, was constructed:
We have used the periodogram^* to rank order all genes in the alpha and cdc28 experiments. Periodogram uses Fourier analysis to determine which genes cycle during the experiment. For both experiments we used the cell cycle duration supplied in the Spellman paper (64 minutes for alpha and 85 minutes for cdc28). FV and FC28 consisted of the top 500 genes according to the ranked lists of alpha and cdc28 respectfully. In order to generate a consensus set from both datasets we summed the rank of the gene in both lists (so that a gene that was ranked 50 in alpha and 34 in cdc28 received a score of 84). We then selected the 500 genes with the lowest score and used these as our consensus set which we denoted in the paper as FCOMB.
*: See Ref 21 in paper: Wicher, Fokianos and Strimmer, Bioinformatics 20:5-20, 2004.
Supplementing Fig 3(b) in the paper, here are more figures that depict the cycling genes found by our method and also those cycling genes which were missed if all available time-points are not used. Legend:- Dots: expression values; dashed lines: profiles using 20 time-points; solid lines: profiles using 24 time-points
- Example of cycling genes which can be found using only 20 (out of 24) time-points: Fig #1 , Fig #2 , Fig #3 , Fig #4.
- Cycling genes where all 24 time-points are necessary to identify them as cycling: Fig #1, , Fig #2, , Fig #3. Note that even in these genes the recovered expression profile using only 20 time-points, is very similar to the profile recovered using all 24 time-points.