PowerPoint Presentation

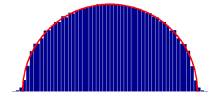
Wigner’s Semi-Circle

vThe classical & most famous rand eig theorem

vLet S = random symmetric Gaussian

vMATLAB: A=randn(n); S=(A+A’)/2;

vNormalized eigenvalue histogram is a semi-circle

vPrecise statements require n®¥ etc.

n=20; s=30000; d=.05; %matrix size, samples, sample dist

e=[]; %gather up eigenvalues

im=1; %imaginary(1) or real(0)

for i=1:s,

a=randn(n)+im*sqrt(-1)*randn(n);a=(a+a')/(2*sqrt(2*n*(im+1)));

v=eig(a)'; e=[e v];

end

hold off; [m x]=hist(e,-1.5:d:1.5); bar(x,m*pi/(2*d*n*s));

axis('square'); axis([-1.5 1.5 -1 2]); hold on;

t=-1:.01:1; plot(t,sqrt(1-t.^2),'r');